On permutation symmetries in Bayesian neural network posteriors: a variational perspective

Abstract

The elusive nature of gradient-based optimization in neural networks is tied to their loss landscape geometry, which is poorly understood. However recent work has brought solid evidence that there is essentially no loss barrier between the local solutions of gradient descent, once accounting for weight-permutations that leave the network’s computation unchanged. This raises questions for approximate inference in Bayesian neural networks (BNNs), where we are interested in marginalizing over multiple points in the loss landscape.

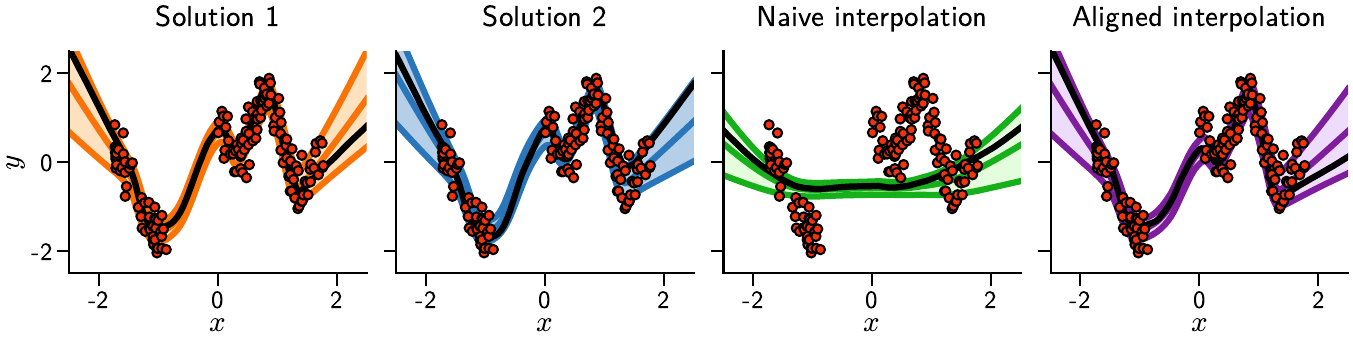
In this work, we first extend the formalism of marginalized loss barrier and solution interpolation to BNNs, before proposing a matching algorithm to search for linearly connected solutions. This is achieved by aligning the distributions of two independent approximate Bayesian solutions with respect to permutation matrices. We build on the results of Ainsworth et al. (2023), reframing the problem as a combinatorial optimization one, using an approximation to the sum of bilinear assignment problem. We then experiment on a variety of architectures and datasets, finding nearly zero marginalized loss barriers for linearly connected solutions.

Key Contributions

1. Extension to Bayesian Neural Networks: We extend the formalism of marginalized loss barriers and solution interpolation from deterministic neural networks to Bayesian neural networks, enabling the study of connectivity in the space of posterior distributions.

2. Distribution Alignment Algorithm: We propose a novel matching algorithm that aligns the distributions of two independent approximate Bayesian solutions with respect to permutation matrices, addressing the permutation symmetry problem in BNN posteriors.

3. Combinatorial Optimization Framework: We reframe the alignment problem as a combinatorial optimization task, building on recent advances and using an approximation to the sum of bilinear assignment problem for computational efficiency.

4. Empirical Validation: Through extensive experiments on various architectures and datasets, we demonstrate that linearly connected solutions in BNNs exhibit nearly zero marginalized loss barriers, extending similar findings from deterministic networks.

Methodology Overview

1D Posterior Alignment Visualization

Marginalized Loss Barriers in BNNs

Traditional analysis of loss landscapes focuses on deterministic neural networks. Our work extends this to the Bayesian setting where we work with distributions over parameters rather than point estimates. The key insight is that permutation symmetries that leave network computation unchanged must be properly accounted for when studying connectivity between different posterior modes.

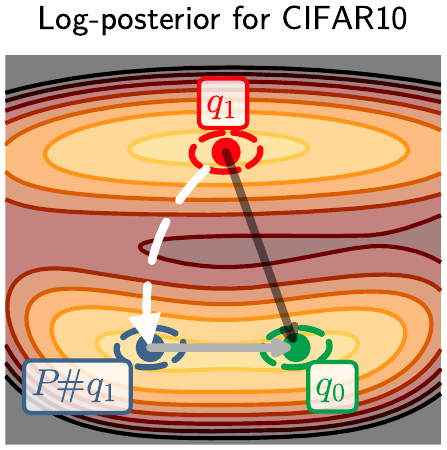
Distribution Alignment via Permutation Matching

Posterior Visualization

The core technical contribution is an algorithm that finds optimal permutation matrices to align two independently trained BNN posteriors. This alignment is crucial because:

• Neural networks exhibit permutation symmetries due to identical neurons
• Different training runs may discover the same functional solution but with permuted parameters
• Proper alignment reveals the true connectivity structure in the loss landscape

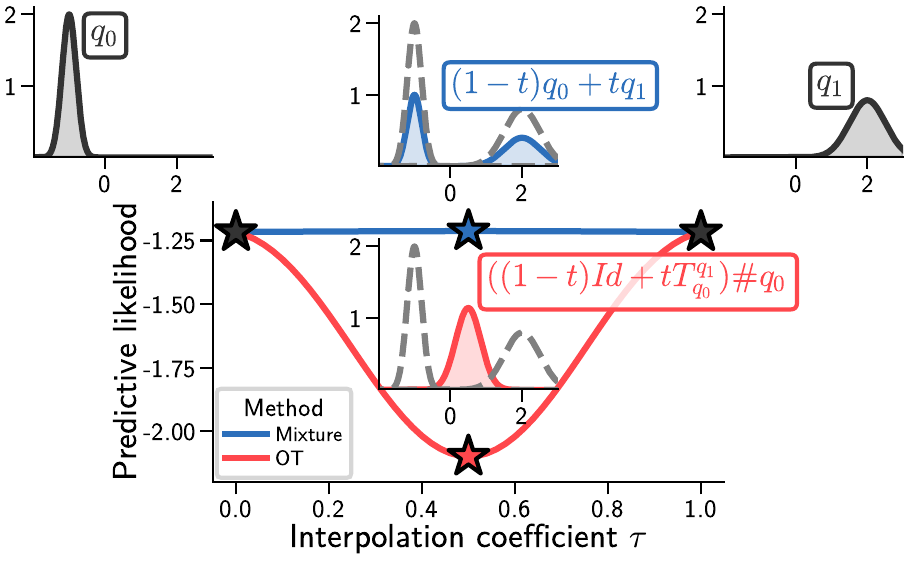
Optimal Transport vs Mixture Approaches

Mixture vs Optimal Transport Comparison

We compare different approaches for combining and aligning posterior distributions:

1. Mixture approaches: Simple averaging of distributions
2. Optimal transport methods: More sophisticated alignment using Wasserstein distances
3. Our permutation-based method: Explicit handling of symmetries through combinatorial optimization

Experimental Results

Our experiments span multiple architectures and datasets:

• Multi-layer Perceptrons (MLPs) on MNIST, Fashion-MNIST, and CIFAR-10
• ResNet-20 architectures on CIFAR-10 and CIFAR-100
• Various network widths and training configurations

Key Findings

1. Near-zero barriers: After proper alignment, we observe marginalized loss barriers close to zero between independently trained BNN posteriors
2. Architecture independence: Results hold across different network architectures (MLPs, ResNets)
3. Dataset generality: Consistent findings across multiple datasets and tasks
4. Computational efficiency: Our approximation scheme makes the alignment procedure practical for realistic network sizes

Implications

This work has several important implications:

• Theoretical understanding: Provides new insights into the loss landscape geometry of Bayesian neural networks
• Practical BNN training: Suggests that different training runs of BNNs may be more connected than previously thought
• Ensemble methods: Informs the development of better ensemble techniques that account for permutation symmetries
• Continual learning: Relevant for understanding how to combine knowledge from different learning phases

The results suggest that the apparent complexity of BNN posterior landscapes may be largely due to permutation symmetries rather than fundamental disconnectedness of solutions.