Scaling Laws for Uncertainty in Deep Learning

Abstract

Deep learning has recently revealed the existence of scaling laws, demonstrating that model performance follows predictable trends based on dataset and model sizes. Inspired by these findings and fascinating phenomena emerging in the over-parameterized regime, we examine a parallel direction: do similar scaling laws govern predictive uncertainties in deep learning? In identifiable parametric models, such scaling laws can be derived in a straightforward manner by treating model parameters in a Bayesian way. In this case, for example, we obtain O(1/N) contraction rates for epistemic uncertainty with respect to the number of data N. However, in over-parameterized models, these guarantees do not hold, leading to largely unexplored behaviors.

In this work, we empirically show the existence of scaling laws associated with various measures of predictive uncertainty with respect to dataset and model sizes. Through experiments on vision and language tasks, we observe such scaling laws for in- and out-of-distribution predictive uncertainty estimated through popular approximate Bayesian inference and ensemble methods. Besides the elegance of scaling laws and the practical utility of extrapolating uncertainties to larger data or models, this work provides strong evidence to dispel recurring skepticism against Bayesian approaches: “In many applications of deep learning we have so much data available: what do we need Bayes for?”. Our findings show that “so much data” is typically not enough to make epistemic uncertainty negligible.

Key Contributions

Overview of Uncertainty Scaling in Deep Learning

1. Empirical Study: We provide a comprehensive evaluation of predictive uncertainties using a variety of uncertainty quantification (UQ) methods across different architectures, modalities, and datasets. To the best of our knowledge, this is the first study to consider scaling laws associated with any form of uncertainty in deep learning.

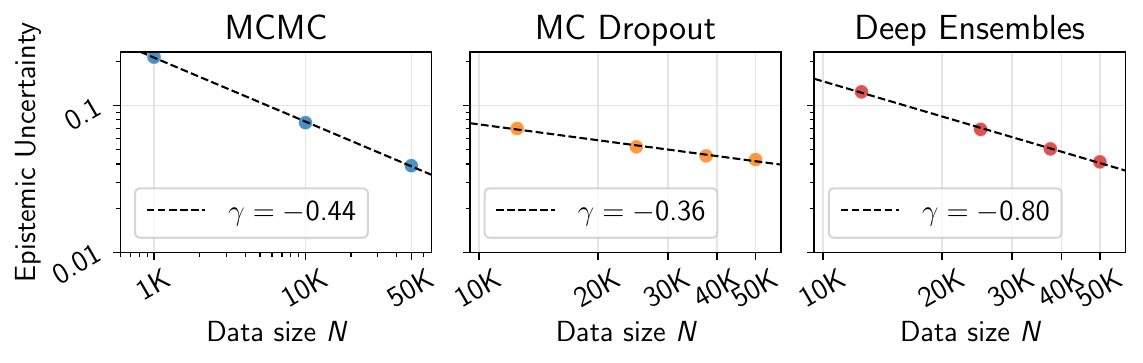
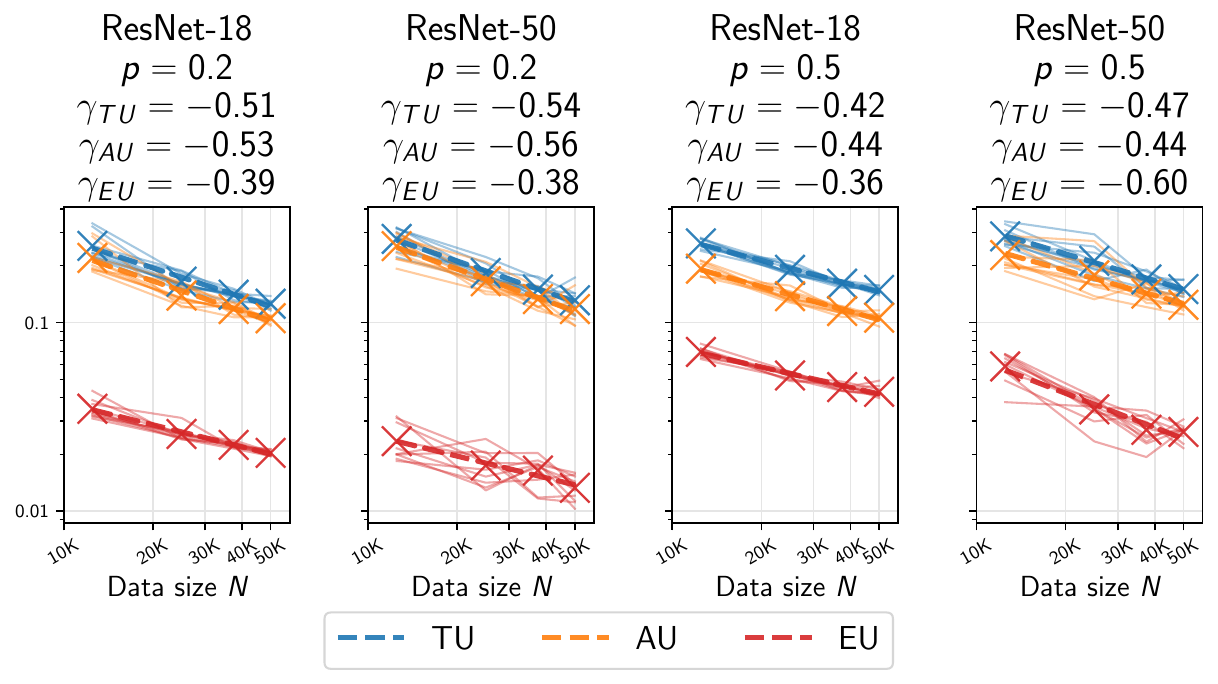
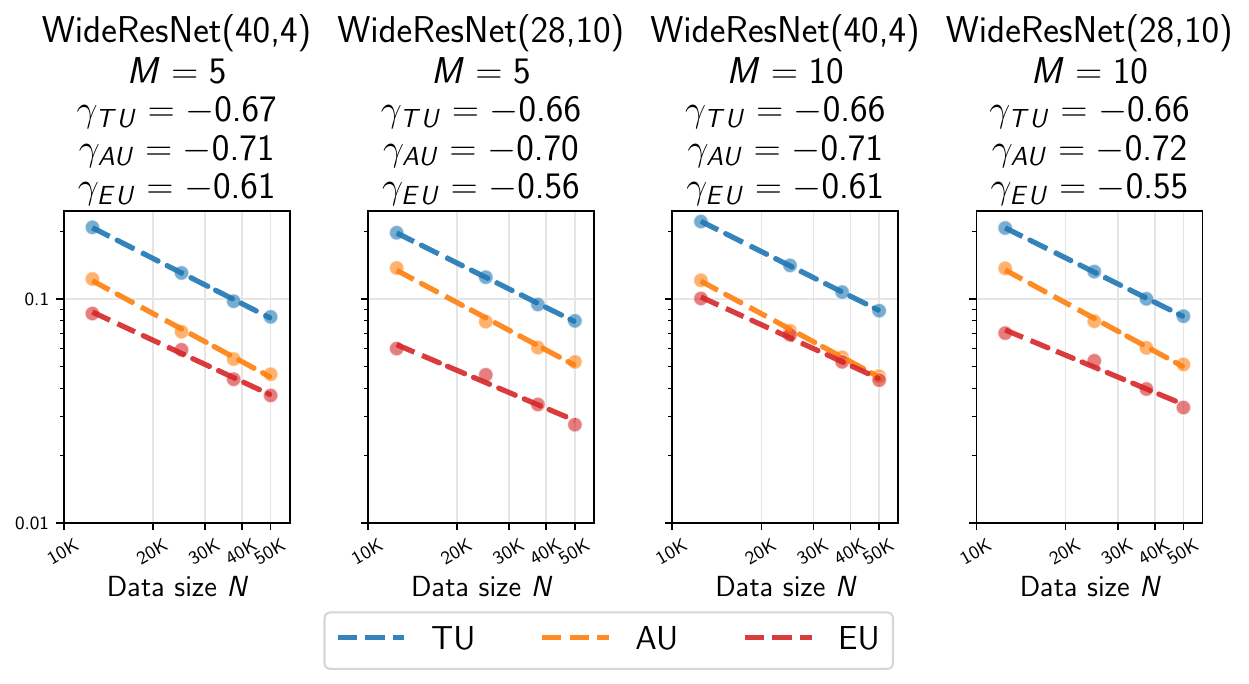
2. Scaling Patterns: We empirically demonstrate that predictive uncertainties evaluated on in- and out-of-distribution data follow power-law trends with the dataset size. This allows us to extrapolate to large dataset sizes and to identify data regimes where UQ approaches remain relevant to characterize the diversity of the ensemble to a given numerical precision.

3. Theoretical Insights: We derive a formal connection between generalization error in Singular Learning Theory and total uncertainty in linear models. This novel analysis provides an interesting lead to explain the scaling laws observed in the experiments for over-parameterized models.

Methodology Overview

Our investigation spans a wide matrix of experimental configurations, exploring combinations across architectures, datasets, and UQ setups. We evaluate several uncertainty quantification methods:

• MC Dropout: Simple and universal baseline with connections to variational inference
• Deep Ensembles: Multiple independently trained networks providing robust uncertainty estimates
  
• Gaussian Approximations: Including Laplace approximations and variational inference
• MCMC Methods: Gradient-based sampling methods like SGHMC and Langevin dynamics
• Partially Stochastic Networks: Inferring only subsets of model parameters

Experimental Results

Uncertainty Scaling Results for ResNet and WideResNet

Our experiments demonstrate consistent power-law scaling behaviors across different architectures and datasets:

Vision Tasks

• CIFAR-10/CIFAR-100: Systematic evaluation with ResNet, WideResNet, and Vision Transformer architectures
• ImageNet-32: Large-scale validation of scaling behaviors
• Out-of-Distribution: Testing on corrupted datasets (CIFAR-10-C, CIFAR-100-C)

Language Tasks

GPT-2 Results on Algorithmic Dataset

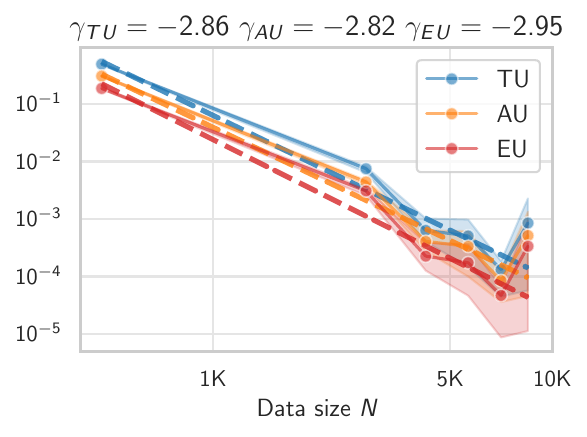
• Algorithmic Datasets: GPT-2 trained on modular arithmetic problems showing clear scaling patterns after extensive training
• Large Language Models: Experiments with Phi-2 using Bayesian LoRA fine-tuning

Deep Ensembles Scaling Results

Theoretical Connections

We establish formal connections between uncertainty scaling and generalization theory through Singular Learning Theory (SLT). For Bayesian linear regression, we show that:

1. Total Uncertainty decomposes into aleatoric (data noise) and epistemic (parameter uncertainty) components
2. Generalization Error in SLT framework relates directly to predictive uncertainty
3. Power-law Scaling emerges naturally from the theoretical analysis, providing insights into the empirical observations

The theoretical framework suggests that the effective dimensionality of the model, as characterized by SLT, plays a crucial role in determining uncertainty scaling behaviors.

Implications and Future Work

Our findings have important implications for:

• Practical UQ: Understanding when epistemic uncertainty becomes negligible and ensemble collapse occurs
• Resource Planning: Extrapolating uncertainty behaviors to larger datasets and models without expensive retraining
• Bayesian Deep Learning: Providing strong evidence against skepticism about Bayesian approaches in large-data regimes

This work opens several avenues for future research, including investigating uncertainty scaling with respect to model parameters and computational budget, and developing more sophisticated theoretical frameworks to explain the observed phenomena.